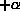 として評価します。電子メールで提出でき
ない場合は、ワープロの出力でも同等とみなします。その旨を書いて下さい。
両方とも利用できない場合、
として評価します。電子メールで提出でき
ない場合は、ワープロの出力でも同等とみなします。その旨を書いて下さい。
両方とも利用できない場合、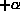 の評価がほしい人は、A304,A288まで相
談に来て下さい。
の評価がほしい人は、A304,A288まで相
談に来て下さい。
1. 集合Aから集合Bへの関数全体の集合が、どのようなものになるかをA,Bのうち一つ以上が空集合の場合について説明せよ。
2. CPOからCPOへの連続関数全体がCPOになることを示せ。
3. 位相空間において、コンパクト集合の連続関数による像がコンパクトになることを証明せよ。
4. コンパクトハウスドルフ空間の空でない閉集合全体に集合の包含関係で、含む 方が小さいという関係を入れると、CPOになることを証明せよ。
5. コンパクトハウスドルフ空間上の連続関数が、CPO上の連続関数を定義するこ とを示せ。
6. 授業で習ったこと、計算機科学の理論で自分で勉強したことから問題をつ くって提出せよ。回答者の理解度を把握できる問題とすること。
7. 授業に対する感想、批判、改善点を述べよ。
提出先:
電子メール sakura@i.h.kyoto-u.ac.jp
あるいは A304 桜川
提出期限:9月末日 多少の遅れは認めるのでめげずに出すこと
電子メールで提出すると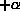 として評価します。電子メールで提出でき
ない場合は、ワープロの出力でも同等とみなします。その旨を書いて下さい。
両方とも利用できない場合、
として評価します。電子メールで提出でき
ない場合は、ワープロの出力でも同等とみなします。その旨を書いて下さい。
両方とも利用できない場合、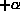 の評価がほしい人は、A304,A288まで相
談に来て下さい。
の評価がほしい人は、A304,A288まで相
談に来て下さい。