Table of Contents¶
Julia+Jupyterによるプログラミング ほんの入り口¶
ここではJupyter Notebookでプログラミング言語Julia(マニュアル)を用いて演習を行います。少ない時間でプログラムとは何であるかを原理的に理解することと、文房具としてのプログラミングをある程度マスターすることを目的としています。本格的なプログラミングを学ぶためにはそれぞれのプログラミング言語の演習を履修することをお勧めします。 Juliaはマクロがあることが特徴の一つとなっていますがこの資料では説明していませんし、十分にその特徴を説明しきれていません。
Jupyter Notebookとはプログラムとその実行結果(値(文字列含む)、グラフ、表形式)、文章(説明)を混在させて編集・表示を行えるツールです。Jupyterのデータの処理を行うプログラムはサーバ方式で動作し、それにwebブラウザから接続して使います(OSのメニュー等からJupyter Notebookを起動すれば自動的にブラウザが立ち上がってローカルに動作するJupyerのサーバに自動的に接続します)。教育環境のWindowsにJuliaの処理系がインストールされていたとしても、うまく動作しなかったり、Jupyter notebookとはうまく動作しない場合があります。しかしフリーソフトウェアであり、BYODのPCに無料でインストール可能です。
Juliaのインストール方法¶
Juliaがインストールされていない場合、インストールしないとJulia言語のプログラムを実行できません。当然ながらインストールは一回行えばよいです。またJuliaをインストールするとJupyterも同時にインストールされます。別にJupyterもインストールする必要はありませんので注意してください。
以下、まずはインストールからコンソールでの初回起動までをOSごとに記し、その後Jupyter notebookを使うための追加のインストール項目を記します。なお表示されるversionや種々のデザイン等は時期によって異なります。あるいは全く違った方法でインストールするように変わる可能性もありますのでもしそうならリンク先を読むなり検索するなりして調査してください。注意点として、webブラウザでファイルをダウンロードする場合にはウイルススキャナのパターンファイルを更新してからダウンロードしたファイルを必ずスキャンするようにしてください。
JuliaをBYODのPCにインストールする場合にはファイルシステムの空き領域が数GB程度あれば使えます。 しかし教育用計算機など、ファイル領域の制限が強いシステムを利用する場合には注意が必要です。 Juliaを自分でインストールするか、 或いは初めから共通領域にインストールしてあってもJuliaの追加ソフトウェアをユーザ領域にインストールする場合には、 ユーザ領域の制限範囲内に収まらない可能性があります。 無理にインストールすると容量制限のために動作がおかしくなる場合がありますので、 そういう場合にはインストールを避けてください。
Windows¶
まずPlatform Specific Instructionsを参照してください。 Julia downloadsからWindows版をダウンロードします。ダウンロードしたインストールのための実行ファイルを実行し、インストールしてください。 インストールの方法は2種類あります。
- 一人が利用するためのインストール。
- 全てのユーザが利用するためのインストール。
1.の場合にはダウンロードファイルを単にダブルクリックするなどして実行し、指示に従ってインストールしてください。2.の場合には右クリックして[管理者として実行]を選び、インストール先のディレクトリを指定してインストールしてください。後者の場合には管理者権限が必要です。一般にはこういったソフトウェアをインストールする際に、インストールするのは管理者権限で共通の場所にインストールした方が複数人使用の場合にディスク使用量を節約できます。
またその場合、ソフトウェア本体を信用する上での話として、一般ユーザで使用した方がウイルス感染時に感染が限定されやすくなります。以下は2.の場合にインストール先としてC:\Program Filesを指定したところです。
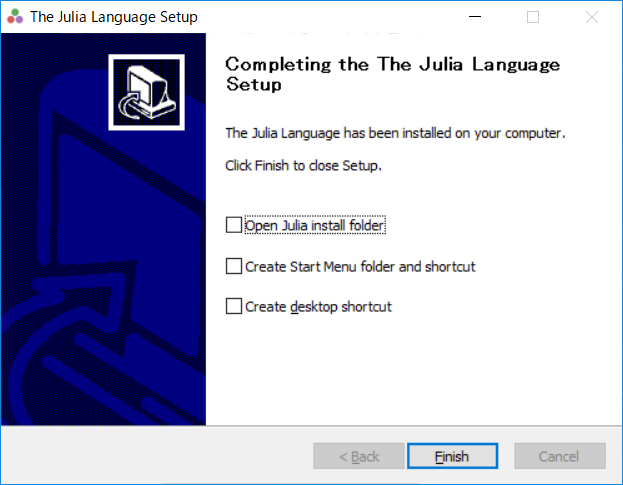
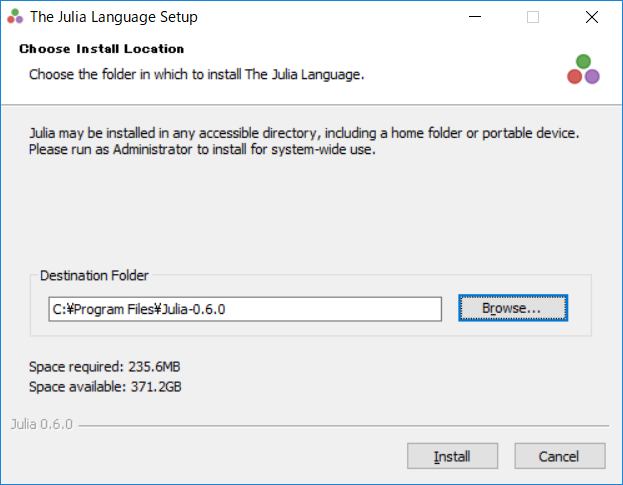インストールの作業が(ほぼ)終了すると以下の表示となります。これはversion0.60の場合の表示です。
インストール後はスタートメニューからJuliaを起動できます。起動すると以下のウィンドウが表示されます。
但し、version 0.6では 全てのユーザが利用するためのインストール が最終的にうまく動作しない場合がありました。 また、プロキシが動作せず、 パッケージのインストール(後述のPkg.add)がうまくいかない場合があるようです。 該当するversion、環境の場合には注意してください。
外部記憶装置へのインストール¶
WindowsでUSB3メモリやUSB3接続のSSDなどの外部記憶装置にJuliaをインストールして利用することが可能です。 ただしメディアセンターのPCでこれを行うと、時間がかかりすぎます。 メディアセンターのPCで、Juliaがインーストールされていない場合、ユーザエリアが少ないため、 外部記憶装置にインストールしないとJuliaを利用できません。 従って、速いBYODのPCなどでUSB3接続のSSDにインーストールし、それを直接センターのPCに接続して利用するか、 USBメモリ等にコピーしてそれを接続し、利用することになります。
以下では外部記憶装置がF:\にマウントされていると仮定して説明しています。
まず、Juliaのインストール時に外部記憶装置を指定します。
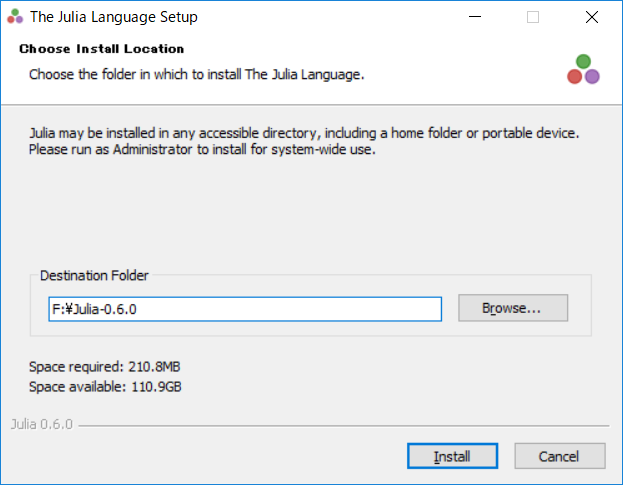インストール後には次のように指定します。これはversion0.60の場合で、versionにより指定方法が異なる可能性があります。
その後F:\julia.batをテキストエディタで作成し、内容を以下のようにします。
set JULIA_PKGDIR=F:\dot.julia
cd F:\
F:\Julia-0.6.0¥bin\julia.exeフォルダF:\Juliaも作成し、結果的に以下のようになります。
ただしAnaconda関係のフォルダ・ファイルも入っています。
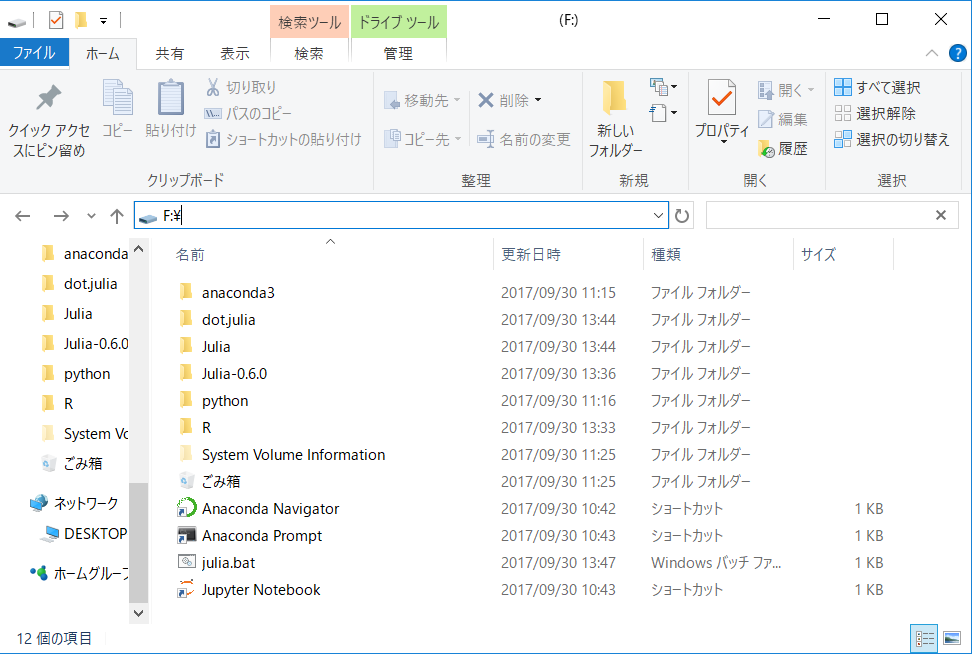その後F:\julia.batをダブルクリックしてJuliaを起動し、次のコマンドを入力します。
手許のPCでは5分ほどかかりました。なおversion0.7以降の場合にはパッケージの扱いが変更されています。少し下の説明を読んでください。
julia> Pkg.init()↩︎
これでとりあえずのインストールは終了です。
ただし、教育環境のPC等で使うために、
これ以降のパッケージ等のダウンロード・インストールを避ける(教育環境のPCで行うと時間がかかります)には、
以下のようにしてパッケージをインストールし、プリコンパイルを行なっておく必要があります。
具体的にはF:\dot.juliaの中にインストールされ、更新されます。
julia> Pkg.add("IJulia")↩︎
JupyterからJuliaを使うにはここまででよいです。 次の部分は以下で説明するJupyter notebookを動作させてそこから行うことも可能です。
julia> using IJulia↩︎
julia> Pkg.add("PyPlot")↩︎
julia> using PyPlot↩︎
julia> Pkg.add("DataFrames")↩︎
julia> using DataFrames↩︎
julia> Pkg.add("Luxor")↩︎
julia> using Luxor↩︎
julia> Pkg.add("ImageMagick")↩︎
julia> using ImageMagick↩︎
最後にjuliaを抜けます。
julia> quit()↩︎
なおversion0.7以降の場合にはPkg.addなどのコマンドを使う代わりにパッケージを扱うためのモードが用意されています。
その場合Pkg.で始まるコマンドごとに以下のように入力するのが一つの方法です。
julia>]
(v1.0) pkg>コマンド↩︎
.
.
(v1.0) pkg>BS (バックスペース。元のモードに戻る。)
julia>
「コマンド」の部分は、例えばPkg.add("ファイル名")の場合、add "ファイル名"とします。連続してPkg.コマンドを入力する場合には一々元のモードに戻す必要はありません。
別の方法は、Pkgというパッケージを導入することです。
そうするとそれ以降はPkg.という接頭辞のコマンドを利用できます。
julia>using Pkg↩︎
外部記憶装置に上記のようにインストールした場合にはF:\julia.batをダブルクリックしてJuliaを起動します。
また、AnacondaのJupynter Notebookを起動するとJuliaカーネルを選択できるようになっている場合があります。
なお外部記憶装置へのインストールの説明の後半部分は、後述の3者共通の追加の作業の部分を含んで記述しています。
Mac¶
まずPlatform Specific Instructionsを参照してください。
macOS Sierra: アプリケーションをインストールするやそこからのリンク先を読んだり、やはり検索してインストールについて記述しているwebページを読んでください。
Julia downloadsからMacOS版をダウンロードします。
管理者権限のあるユーザでダウンロードした.dmgファイルをダブルクリックしてマウントし、/Applicationにインストールするアプリケーションをコピーします。具体的には下図のJuliaのアイコンを横のApplicationsにドラッグ&ドロップします。なおMacではApp Store以外で入手したソフトウェアは、そうして問題なければ、管理者権限のあるユーザでインストールし、使用するのは通常ユーザにした方が望ましいです。こうすると通常ユーザはアプリケーションを書き換えられなくなりますのでウイルス感染しても感染範囲を限定できる場合があります。ネットサーフィン等は通常ユーザで行うべきです。
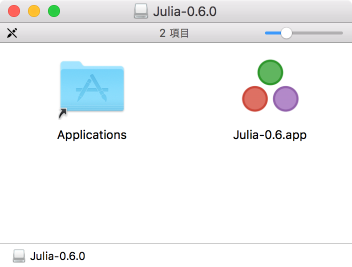この後Juliaを使用するユーザでloginします。以下はアプリケーションのJuliaのアイコンです。
アイコンをダブルクリックするなどして初回起動するとJuliaのコンソールが現れます。
Mac版のJuliaで上のインストールの仕方をした場合の問題点は、 追加のソフトウェアパッケージをある程度インストールすると、 ユーザ毎に数GBのファイル領域が使用されるということです。 これはMac版に限らないかもしれません。
ubuntu¶
通常のubuntuのリポジトリにJuliaがあるのでそれを通常通りインストールするのが最も楽です。 しかしこの方法では例えば今回の調査時には、version0.4.5のものが入りました。 これはかなり古めであって例えば内包表記が使えず、この資料の例題の一部にも動かないものが出てきます。 仮想端末で以下のようにリポジトリの指定を追加するとversion0.5.3になり、ましになりました。
$sudo add-apt-repository ppa:staticfloat/juliareleases↩︎
$sudo add-apt-repository ppa:staticfloat/julia-deps↩︎
リポジトリを追加する場合もしない場合も以下を行うとインストールできます。
$sudo apt-get update↩︎
$sudo apt-get -y install julia↩︎
但しリポジトリを追加した場合、旧いJuliaが既に入っていると衝突してインストールがうまくいかない場合があるようですので、 旧いJuliaをアンインストールして問題なければ、次の2つのコマンドが何をするか理解した上で実行してからインストールし直してください。
$sudo apt-get remove julia↩︎
$sudo apt-get autoremove↩︎
どうしても最新版を使いたい場合にはJuliaのホームページからダウンロードしてきてインストールする必要があるようです。 まずPlatform Specific Instructionsを参照して インストールしてください。
インストール終了後はOSの通常のアプリケーション起動方法でJuliaのコンソールを起動できるはずです。
3者共通の追加の作業¶
上記インストールが終わればコンソールからJuliaを利用できますが、Jupyter NotebookからJuliaを利用するには若干追加の作業が必要になります。
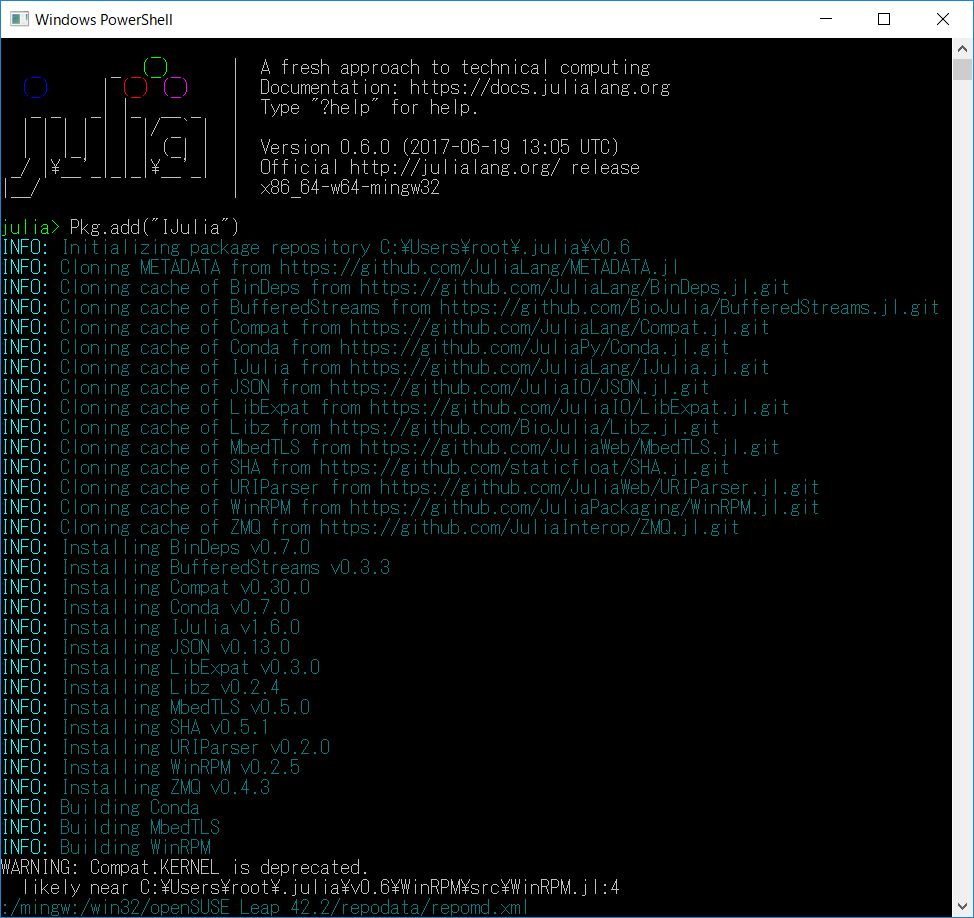
まずJuliaをコンソールから使うように起動します。例えばメニューから起動できる場合にはそうしてください。Juliaのコンソールに以下のコマンドを入力します。これに限らずPkg.add(-)はファイル群をネットワークを介してダウンロードしてインストール作業を行うので実行にはある程度時間がかかります(既にインストールされている場合にはそれほど時間はかかりません)。終了したらプロンプトが出てきます。
julia>Pkg.add("IJulia")↩︎
あるいはversion0.7以降の場合には、以下のように入力します。
julia>]
(v1.0) pkg>add "IJulia"↩︎
.
.
(v1.0) pkg>BS (バックスペース)
julia>
別の方法は、Pkgというパッケージを導入することです。
そうするとそれ以降はPkg.という接頭辞のコマンドを利用できます。
julia>using Pkg↩︎
なお以降ではversion0.7以降の場合の説明を省略します。
通常この作業はJuliaのインストールごとに一回だけ行います。
JuliaやJupyterの起動ごとに行う必要はありません。
以下はWindowsでの表示の例です。
既にJupyterがインストールされていた場合¶
既にPCにJupyterがインストールされて正常に動作している時に、JuliaをインストールするとJuliaのkernelが旧システムに追加されて旧システムの通常使用時にkernel選択肢にJuliaも出るようになる場合があるようです。例えばAnacondaがインストールされているとそうなる場合が多いようです。もしそのようになったならそのままで構いません。またこの場合には旧システムからJuliaのnotebookを起動して構いません。そうならなかった場合にはJuliaのkernelの設定ファイルを旧システムのJupyterが読める場所にインストールする必要があると考えられます。しかしその場合はここでの説明の対象外としたいと思います。
Jupiter Notebookの起動と終了・利用方法¶
この段落で説明する起動方法は別ページで説明と 異なっていますので注意してください。Jupyterを利用するシステムとしてJuliaのみをインストールした場合にはこの段落の方法を取ることになります。そうでない場合には他のシステムでのJupyterの起動方法も動作する場合があります。
JupyterからJuliaを使うように起動する方法はいくつかありますが、ここではコンソールのJuliaからJupyterを起動する方法を紹介します。
まずメニューから選択するなどしてJuliaをコンソールから使うように起動します。
Juliaのコンソールに次のように入力します。
但しインストールの節のようにIJuliaがPkg.add(-)により既にインストールされていることを仮定しています。
julia>using IJulia↩︎
julia>notebook()↩︎
するとwebブラウザが起動してJupyterの表示が出ます。以降はJupyturサーバを停止する前まで、webブラウザでJupyter Notebookを利用することになります。
なおエラーが出る場合、以下のように再コンパイルを行うとうまく動作する場合があります。
julia>Pkg.build("IJulia")↩︎
julia>notebook()↩︎
Jupyter Notebookの利用方法については別ページを参照してください。但し、この資料のプログラムを動かすには、新しいnotebookを作るときのメニューでkernelをJuliaとするか、あるいは後で[kernel]メニューから[Change Kernel]→[Julia ...]を選ぶ必要があります。これらのメニューにJuliaの項目が表示されない場合、Juliaのkernelが正しくインストールされていません。Notebookの右上にJuliaの言語名が表示されていることを確認してください。
Jupyterを終了するには別ページに従って全てのnotebookを閉じてから、Juliaのコンソールで例えば[ctrl]+cを入力して停止するか訊いてくる場合にはyを入力します。するとJupyterのサーバが停止します。
Juliaのコンソールを停止するにはコンソールのウィンドウを消します。
[ctrl]+c等が効かなければ最初からコンソールウィンドウを消すことになります。
学習方法¶
このページを表示しながら、プログラムのコード部分(In [ ]:の右側枠内の部分)を順にJupyterのセル(やはり枠内の部分。プログラムなのでCode属性にする)に手入力するかコピー&ペーストし、実行します。或いは授業中に提示する予定の、notebookのデータファイルをuploadすることで、直接実行することが可能になります。但し提出課題の部分は自分で入力するなり変更するなりする必要があります。
課題の提出方法¶
課題の回答プログラムを作成して動作確認したらコピー&ペーストによりプレーンテキストのファイルとして提出してください(次回以降も同様)。
ファイル名: 課題提出用ID-課題番号.jl
ファイル名の例: e20000-kadai09.jl
課題番号は課題ごとに変わりますし、左側の課題提出用IDは各自異なります。 画像ファイルなど、プログラムでない内容のファイルの場合には拡張子の部分を例えばpngとするなど、適切なものにしてください。
注意点:¶
- 適宜コメントを記述してください。
- プログラムについては、提出前に動作することを必ず確認してください。
- ファイルの冒頭にもコメントとして課題提出用IDと課題番号を記してください。
- ファイル中に、第三者が個人を特定できる情報を書かないでください。
- ファイル名はすべて半角にしてください。
- 上記注意点が守られていない場合、評価対象とならない場合があります。
最初のプログラム¶
下の「1+2」はこれで一つのプログラムです。これを実行する(評価する)にはマウスでクリックして下のセルを選択し、(存在する場合は)ウィンドウ上方の[>|]のボタンをクリックするか、SHIFT+returnキーを押します。Out[..]: 3というように値3が表示されれば正常に動作しています。
1+3
次のセル中に加減乗除(+-*/)による数式を書き、同様に実行してみてください。セルの中を書き直して再実行できます。
10+4*(3/4+100)+1011
これはJulia(ドキュメンテーション)というプログラミング言語のプログラムとして対話的に実行しています。一応ウィンドウ右上に[Julia ...]などと表示されていることを確認してください。プログラムの実行の仕方としてバッチ式と対話式という方式があり、前者は(複数の時もありますが)一つの定まったプログラムにデータを与えて処理を行う方式です。後者はプログラムの処理系にプログラムの断片を入力しつつ、対話的に小さいプログラムの実行と結果の表示を繰り返し行う方式です。
対話的に実行する方がとっつきやすいので、この資料では対話的に実行する方法で解説を行います。ただし、Jupyterの場合セルごとに実行を行うため、実行の順序によって処理系(プログラムの実行を行うプログラム達。本体部分はかなりの部分が機械語でできていたりします。実行する対象のプログラムはJulia等の、人間が理解しやすい高級言語で書かれたものです。大きく分けてコンパイラ方式とインタプリタ方式があります)の状態が異なる場合があります。また、そもそも実行していないセルがあると、その内容に依存する他のプログラムの断片がうまく動作しない場合がありえますので注意が必要です。これについては後で説明します。
ここでJuliaのversionを確認しておきます。以下ではversioninfo()の値を求めています。
versioninfo() # #から右側はコメントとなる
Julia言語のチュートリアル等を参照する際にはversionが近いものを参照してください。
変数¶
変数はほとんどのプログラミング言語において重要な概念です。変数(variable)とは、何らかのデータを格納する箱だと思ってください。箱には名前があり、それを変数名と言います。後で出てくるように違う箱だが同じ名前が与えられる場合があり、その場合についての理解が必要です。Juliaでの変数名等の名前の付け方は使用可能な変数名・文体表記を参照してください。 やはり後で出てくるように、文字に添え字、^を付けたりギリシャ文字や一部の数学記号の使用も可能になっています。
また、Juliaを含めて手続き型のプログラミング言語ではプログラムの実行途中で値を変更することができる種類の
変数があり、それが計算の状態変化を表します。このようにプログラムの実行途中で値の変化が可能な変数をmutableな変数と言います。変数の箱に値を入れることを代入(assignment)と言い、Juliaの場合には=を使って表します。結果的に左右両辺が等しくなるとは限らず、数学での等式を表しているのではないことに注意してください。
変数には種類があり、どのような種類の変数が使えるかはプログラミング言語により変わります。しかしまずここではそれらのうち大域変数(global variable)という、プログラム(ファイル内)のどこからも参照できる(例外があります)変数のみが出てきます。大域変数についてはそれらの箱はプログラムの実行開始時(あるいはその変数が存在することがわかった最初の時点)からプログラムの実行終了時まで存在し続けます。
以下、上から順番に各セルを実行してみてください。例えばx=式、で式の値を計算し、結果をxに代入します。Juliaでは代入文が値を持つことがわかります。なお#から右側はコメントとして扱われ、この部分は実行されません。
x=11 # 変数xに11を**代入**する
y=23
z=x*y
x
z*z
x=12
z=x*y
z+=3 # z に3を加える
z*=2 # zの値を2倍する
この例のように、変数には値を格納することが出来ます。その後の命令の列が全く同じでも、変数の値によって計算は変わってきます。上から順に実行した場合には最初xの値が11であり、それに依存して決まるzの値は最初253になります。しかしその後xの値が12に変更されてからz=x*yという同じ命令によってzの値は276という異なる値になります。変数は電卓のメモリと同じ用途で用いることが可能です。
上から順に実行した場合、最初のz=x*yでzの値は253になりますが、その後下の方の命令を実行してxの値が異なる値に変化してから(下の方のではなく)最初と同じセルのz=x*yを実行すると、zの値は異なるものとなります。また、x=11やx=12を実行する前にz=x*yを実行するとxの値が定義されていないためにエラーになります。このようにセルの実行順序によってエラーが起きたり変数の値を含めて状態が変化することに注意してください。また、z+=3のように実行の度にzが増加するため実行回数が影響を与える場合もあります。上から順に実行すれば実行回数に関わらず正しく動くようなnotebookとするのが望ましい場合が多いです。
Juliaでは数値以外にも様々なデータを扱います。例えばデータの列である配列や文字列などがあります。データの種類のことを一般にデータ型といいます。プログラムの実行前に式が表すデータの型が定まるようなプログラミング言語を静的型付けの言語と言います。それに対し、データ型が実行前に決まらず、実行時にチェックされる言語を動的型付けの言語と言います。Juliaは一応、動的型付けの言語に分類されます。
静的型付けの言語はプログラムの実行前に、ある種のプログラムのミス(BUG)がないことを自動的にチェックできます。特に強い型付けという種類に分類される言語では、実行前のチェックを通っていればデータ型に関するエラーが実行時に起きないことが保証されます。ただしプログラミングを学ぶ際にデータ型に関する理論をある程度学ぶ必要がありますし、十分広い枠ではありますが、一定の枠に嵌ったプログラムのみを書けることになります。Juliaは動的型付けの言語に分類されます。しかし実行前に型推論(人間が式等の型を指定しなくても自動的に式の型を求める機能)を行い、それに基づいて最適化(プログラムの性能が高くなるような工夫)を行います。但しデータ型のエラーの実行前のチェックは必ずしも行われず、実行時に検出されることになります。
条件判断¶
ここまではほとんど電卓と同じように計算を行ってきただけでした。しかし今から出てくる条件判断と繰り返しは、通常の電卓にはないものであり、計算機を有用な道具とするには必須のものです。Juliaの条件文は以下のような構文になります。改行やインデント(字下げ)はJulia処理系にとってそれほど意味はなく、主に人間にとっての読みやすさのためにあります。但し以下で例えば式1と2を同じ行に記述する場合には間に「;」(セミコロン)が必要です。
構文:
if 条件式
式１ # 条件がtrueであればelseまでの部分が実行される。
式２ # 改行は空白と同じく区切りである。
.
.
else # elseからendの前まではなくてもよい。
式ａ # 条件がfalseであればendまでの部分が実行される。
式ｂ
.
.
end通常、条件式の部分には等しいかどうか(==,!=)大小関係等(<,>,<=,>=)やそれらの組み合わせ(&&,||,!で組み合わせる)等、真偽値をとるような式を記述します。なおelseから対応するendの前までの行はなくても構いません。その場合は条件式がfalseであった場合、条件文内では追加で何も実行されません。またelse後の文a...の部分がまた別のif文になっている場合、インデントのレベルを深くしないための書き方(elseif)があります。これに付いては後で出てきます。
次の2つの具体例では条件部分の真偽により式の値が変化します。==は両辺が等しい時true、等しくない時falseとなります。Juliaではif文そのものが値を持つ場合があることがわかります。
if 1 == 1
x=1
else
x=2
end
if 1 == 0
x=1
else
x=2
end
Juliaでは改行(コメント後を除く)は式の区切りの意味を持ちます。インデントの量は特に意味はありません。従って同じプログラムを下のように記述できます。
if 1 == 0 x=1 else x=2 end
1==1,1==0,1!=0,1>2,true || talse, true && true, !true # 組(tuple)となる
繰り返し¶
Juliaで繰り返し処理を記述する方法は多数あります。ここではそれらのうちの一つ、forによるものを紹介します。
構文:
for 変数 in 範囲
式１ # 変数の値を範囲の中で変えてendまでの式が繰り返し実行される。
式２
.
.
endなおif文やfor文は入れ籠にすることができます。
for i in 1:100 # 1:100は1から100までを意味する。
print(i,' ') # printは引数(ひきすう、argument)の値を出力する。
end
同時代入¶
代入の際に、「,」で区切って複数個の変数に同時に代入できます。これにより例えば変数の値の交換を簡単に記述できます。
x = 1
y = 10
x,y = y,x # 同時代入
函数定義と、変数のスコープ¶
新しい函数を定義することが可能です。例えば二次方程式$ax^2+2bx+c=0$の解(の一つ)を求める函数quadraticは以下のように定義できます。
function quadratic(a,b,c)
return (-b + sqrt(b^2 - a*c))/a # 返り値。a^b はaのb乗
end
以上はPythonなど他のスクリプト言語に近い書き方です。Juliaではもっと通常の数学に近い記述の仕方が許されます。
quadratic(a,b,c) = (-b + √(b^2 - a*c))/a
quadratic(1,3,1)
Unicode文字の使用¶
ここで√ の記号はUnicode文字です。 \sqrt[TAB]とタイプすることで入力できます([TAB]はTABキー)。 同様のやり方でギリシャ文字を入力でき、 また添え字に見える文字を入力したり、^などの補助記号をつけた表示にしたりできます (なおHTMLに変換した場合、一部の表示がうまくいかない場合があります。)。 ギリシャ文字や数学記号の入力方法は$\mathrm{\TeX}$からの連想で大体わかるものも多いです。 入力方法はUnicode Inputにまとめてあります。 Unicode文字をうまく使えばプログラムがすっきり見やすくなり、可読性が増します。 但し環境によってうまく表示されない文字があったり、 色々誤解を招きかねない場合もありますので、 使える場合でも無制限な利用は避けるべきでしょう。 なおMacでは\は¥ときちんと区別して表示されます。日本語キーボードでは[option]+¥で\を入力できます。
δ = 0.01 # \delta[TAB]
x₁ = [2.0,-1.0] # x\_1[TAB] 添え字に見えるが₁自身が一つの文字である。
Δx = δ*x₁ # \Delta[TAB]x = \delta[TAB]*x\_1[TAB]
âx = 1 # a\hat[TAB]x 但し̂ は現状そのままでは名前の最初の文字に使えない。
x² = âx*âx # x\^2[TAB]=a\hat[TAB]x*a\hat[TAB]x このようにもできるが、
Δx,x² # x²が一つの変数なのに、演算を行っているという誤解を招く可能性がある。
局所変数と大域変数¶
変数には局所変数と大域変数があります。 局所変数はある範囲内のみで有効で、たいていの場合実行途中で一時的にしか存在しない変数です。 次の例を見てください。
function test1()
newvariable_fun = 1 # 函数定義の中の場合、代入先の変数は局所変数となる。
end
test1()
newvariable_fun # 未定義なのでエラーとなる。
変数の有効範囲のことをスコープといいます。 この例の場合、newvariable_funという変数のスコープは函数test1の定義内であり、 この変数は局所変数です。大域変数の例は変数の項目を参照してください。
局所変数と同じ名前の大域変数がある場合、それらは函数内部からは基本的に参照できなくなります。大域変数と局所変数で同じ名前の変数がある場合、あるいは函数呼び出しが何重にも重なった場合に同じ変数名の変数が出てくる場合があります。それらは変数名が同じなだけで、「箱」としては別物であることに注意してください。
函数定義中の変数¶
まず、函数定義の仮引数となっている変数はスコープをその定義内とする局所変数です。 それ以外の函数定義中の変数のスコープも基本的には同じです。 但し仮引数でない場合、通常次のような例外があります。 これらの場合、当然外側でその変数名の変数が定義されていないといけません。
- 函数定義内でglobal宣言されている変数。
- 函数定義内で代入先となる文がない変数。
後者の場合、 何も代入されていない局所変数を参照するとエラーとなるため、 通常ありませんから宣言しなくてもわかるというわけです。 但し後者の変数は大域変数になるとは限らず、 外側のスコープの局所変数かもしれません。
x = 0
y = 1
z = 2
function test2()
global y # globalを付ければ大域変数となり、外側と同じ箱となる。
x = 3 # 函数定義の中で代入先になっているためxは別の箱で、局所変数となる。
y = 4
z # zには代入せず参照するだけなので函数定義の外側から継承されて大域変数となる。
end
test2(),x,y,z # 函数定義の外側のxは函数定義中のxと同じ変数名だが別の箱。
for i in 1:10
newvariable_for = 1 # 外側に存在しなければ局所変数となる。
end
newvariable_for # やはり未定義エラー。
ループ中の変数¶
函数定義の場合とは異なり、forのようなループの場合には外側で既に定義されている変数は、 基本的にループの中でもそのまま同じ変数になります。 代入先であっても外側と同じ変数です。 強制的に局所変数にしたい場合にはlocal宣言をします。
x = 0
y = 1
for i in 1:10
local y # yは局所変数だと宣言。
x = 2 # 代入先だがforなのでこれは大域変数。
y = 3 # yは外側の大域変数として存在しているが、local宣言してあるのでこのyは外側と異なる局所変数。
z = 4 # この場合zが外側で定義されていなければ局所変数であり、local zという宣言は必要ない。
end
x,y # xは1に更新されている。forの中のxと同じ箱。一方yは更新されていない。
# もしもzが大域変数として定義されていなければzをここで参照すると当然エラーである。
for文がトップレベルの函数定義中に現れる場合を説明します。 forから対応するendまでに現れる変数は、外側から継承したものとなります。
x = 0
y = 1
z = 2
t = 3
function test(x,y)
local v
for i in 1:10
local y # yはfor内部の局所変数だと宣言。
x = 4 # 代入先だがforなのでこのxは引数のx。局所変数ではある。
y = 5 # yはforの外側の局所変数として存在しているが、local宣言してあるのでこのyは外側と異なる局所変数。
z = 6 # このzのスコープはfor...end内。
v = t # vは局所変数でスコープは函数定義内。tは大域変数。
end # forの内側でzは更新されるが、函数定義のレベルで更新されないのでここでのzは大域変数。
x,y,z,v # 引数のyはfor内部で更新されない。一方vと引数のxは更新される。x,y,vは局所変数。
end
u = test(7,8)
u,x,y,z,t # 大域変数x,y,z,tは更新されない。
if文中の変数¶
ifではスコープが別になりません。
if 1==1
newvariable_if = 1 # この場合は新たな大域変数となる。
else
newvariable_if = 2
end
newvariable_if
Juliaの変数のスコープには独特の部分がありますので、詳しくはScope of Variablesを参照してください。 基本的にはたいていの場合、スッキリとしたプログラムの文面となる方向性といえると思いますが、 少々わかりにくい場合もありえます。
例題: フィボナッチ函数と階乗¶
ここまでの知識で定義できる函数の例題を見てみます。
フィボナッチ函数とはfib(0)=1, fib(1)=1, fib(n)=fib(n-2)+fib(n-1)として再帰的に定義される函数です。自然界のいろいろなところで現れることが知られています。
function fib(i)
x,y = 0,1
for i in 1:i
x,y = y,x+y
end
x
end
fib(0),fib(1),fib(2),fib(3),fib(4),fib(5),fib(6) # この式は値の組みを結果とする
function fact(i) # 階乗を計算する函数
y = 1
for i in 1:i
y *= i
end
y
end
[fact(0),fact(1),fact(2),fact(3),fact(4),fact(5),fact(6)] # この式は配列(リスト)を結果とする。[]ではなく()にして組みとしてもよかった。
Juliaで小さい整数を入力するとInt64として扱われ、それによる演算が行われます。Juniaでは任意多倍長整数演算を行えます。しかしその機能を最初から統合した他の(動的型付けの)多数の高水準言語とは異なり、何も指定しないと64bit演算となる場合が多いため注意が必要となる場合があります。これは動的型付けの言語と同じように使えるにもかかわらず高速演算のための最適化を行えることを売りにしているJuliaでの(たぶん小さい)トレードオフの一つだと考えられます。
fact(30) # 64bit整数演算での桁溢れが起きる例
これを解決する一つの方法は、期待する演算が行われる型に変換することです。
fact(BigInt(30))
あるいはプログラムの方を変えても構いません。
function fact_b(i) # 階乗を計算する函数
y = BigInt(1)
for i in 1:i
y *= i
end
y
end
fact_b(30)
fact_b(300)
グラフ¶
ここでグラフを描く方法を書いておきます。レポートを作成する際などに大変便利な機能であり、定規や色鉛筆などを超える文房具としてプログラムを利用することになります。ただしこの資料の今の進度よりは相対的に難しい概念が出てくる部分があります。
ここではJupyter Notebookにインライン(同じ文章中)で表示するため、Python用のプロットライブラリを使用します。
using Pkg
Pkg.add("PyPlot") # Pythonのプロットライブラリをインストールする。
# これはJuliaのインストール(ユーザ)ごとに一回行えばよく、kernelの再起動ごとに行う必要はない。
なお上のパッケージPyPlotのインストールにはかなり時間がかかる場合があります。
すでにインストールされている場合には時間はかかりませんし、表示も異なります。
これは他のパッケージの場合にも、かかる時間がそれぞれ異なる以外は同様になります。
セルの結果の欄に表示される.logファイルの末尾を観察すると進行しているかどうかをチェックできます。
また~/.julia/などの、Juliaのライブライの格納領域の容量が増えているかどうかでもある程度チェックできます。
# Pkg.add("PyPlot") # PyPlotは既にインストールされていると仮定しているのでコメントアウト。
using PyPlot # グラフを描くためのライブラリPyPlotを読み込む。これはkernelの再起動ごとに1回行えばよい。
r = 0:14 # 0,1,2,3,...,14というhanni
scatter(r,map(fib,r)) # rangeの各値にfibを適用したリストを作り、それにより点をプロットする。
# mapにより函数fibを範囲rに適用し、r中の各値の結果の配列を作って点プロットする。
上の表示にはPyPlotの初回動作の場合に表示されるPrecompileのログが含まれている場合があります。
すでにそういった動作が行われていた場合には表示されません。
これは以下も同様です。
0,14を他の値に変えれば範囲が変わり、fibを他の函数に変えれば表示する函数が変わります。函数定義を他で行なってそれを実行し(読み込ませ)てから変更した上のプログラムを実行すればグラフが書き換わります。
ここでmap(fib,r)は範囲rの各値に対し函数fibを適用した結果の列を作ります。listでそれをscatterの引数として許される形に変換しています。scatterは2つの列を引数とし、それらを座標として点を平面にプロットします。
次の例はもう少し実用に近い例であり、どのように指定すれば表示がどうなるのかわかると思います。
# using PyPlot
r = 0:14
r1 = 1:15
scatter(r,map(fib,r1),color="red",label="fibonatti(x+1)") # colorで色の設定。このように複数のグラフを合成できる。
plot(r,map(fact,r),label="factorial(x)") # こちらは階乗の対数の折れ線グラフ。値の差が大きいので各値の対数を計算している。
legend() # 凡例表示。アルファベットと同様に書くだけでは日本語はうまく表示されなかったりする。
xlabel("x") # x軸ラベル
ylabel("value") # y軸ラベル
title("fibonatti and factorial") # タイトル
yscale("log") # y軸はlogスケール
表¶
グラフではなく表形式で表示してみます。
Pkg.add("DataFrames") # やはりこれは一回実行すればよい。
これはDataFrameをそのまま出力しているだけです。
using DataFrames # このセルは函数定義のセル達の後に実行する
DataFrame(x=0:14,fib=map(fib,0:14),fact=map(fact,0:14))
キーワードの補完¶
Jupyterに限らず、ある種のキーワードを補完する機能がついている場合があります。Jupyterの場合には[TAB]キーにより補完を行います。
これはPython以外のkernelの場合にも大抵使える機能です。
Codeセルでキーワードを途中まで打ち込んで[TAB]キーを押すとそれを先頭とするキーワード候補の選択メニューが表示され、選択できる状態になります。
# 次の行に例えば「r」を入力し、`[TAB]`キーを押すとrで始まるキーワード達の選択メニューが表示される。
r
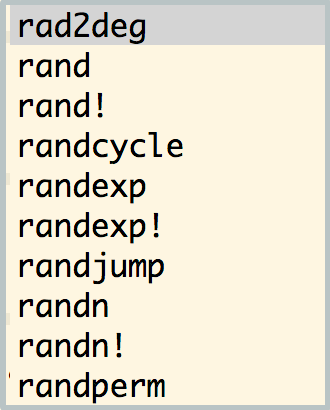
候補が多数ある場合にはスクロールして選択します。
逆にもしも候補が一つもない場合には何も表示されません。
一つしかない場合にはその候補の残りの文字列が自動入力されます。
この機能を指して補完(completion)と呼びます。
長いキーワードを入力する場合に一意的になるまでキー入力後、
[TAB]により補完するとキーストローク数が減り、
誤りも減らせます。
函数・変数等の説明¶
Julia kernelの場合、Codeセルの最初に「?」を入力してその後函数名、変数名を入力し、
[SHIFT]+↩︎を押すと、それについての説明が表示されます。
これはJuliaの場合に使える機能です。
?print
? "concatenate" # ドキュメントから文字列を探索することができる。
最初の課題¶
ここまでに学習した事柄を使って、引数として与えた2つの整数を含めてそれらの間のすべての整数の和を求める函数sum2をJuliaで記述してコピー&ペーストしてメールにて提出せよ。ただし数値演算は和と差のみしか使ってはならない。課題の提出先は従来と同じ、課題提出用IDとkadai07という課題番号をコメントとして冒頭に入れること。拡張子を間違えないように。
# e01234 kadai07 課題提出用IDを書き換え
#
function sum2(x,y)
x+y # 正しいプログラムに書き換えること
end
sum2(-2,1), sum2(1,-3), sum2(10,13), sum2(-100,0)
# -2 -5 46 -5050
# もちろん以下は正しくない値
再帰呼び出し¶
これまでに、フィボナッチ数列や階乗計算のプログラムを例題として示して解説しました。それらは元々再帰的に定義されています。プログラミング言語によっては再帰的に定義された数列等を再帰的なプログラムで表現できる機能を備えています。Juliaにもその機能はあり、例えば次のようにしてフィボナッチ数列や階乗計算を行うプログラムを記述することができます。
fib_r(x) =
if x == 0 0
elseif x == 1 1 # if文の最初の条件を満たさない時にelseifの条件がチェックされる
else fib_r(x - 1) + fib_r(x - 2) # 再帰呼び出し。
end
fib_r(0), fib_r(1), fib_r(2), fib_r(3), fib_r(4), fib_r(5)
fact_r(x) =
if x == 0 1
else x*fact_r(x - 1) # 再帰呼び出し。
end
fact_r(0), fact_r(1), fact_r(2), fact_r(3), fact_r(4), fact_r(5)
このように、fib_rやfact_r自身の定義の中でまたそれらを呼び出すことを一般に再帰呼び出し(retursive call)と呼びます。これもプログラミングにおける重要な概念の一つです。前に例題とした再帰呼び出しによらないプログラムと比較してみてください。ただしfibについては、再帰呼び出しのfib_rの方は非常に効率の悪いものとなっています(なぜでしょうか)が、同じ再帰呼び出しでも効率の良いプログラムを書くことも可能であることを申し添えておきます。
再帰呼び出しのプログラムを書くときの考え方¶
Juliaのような手続き型の言語(ここでは変数への代入文があり、計算状態を変化させる操作の列、即ち手続きとしてプログラムを記述する種類のプログラミング言語を手続き型としています。もちろんJuliaで函数的にプログラムを書いてゆくことも可能でしょう)の場合には、再帰呼び出しのプログラムを書く際に、一般には「再帰呼び出しを行う」という操作を行うことと、その時の状態を意識する場合が多いかもしれません。しかしこれまでに出てきたようなフィボナッチ函数や階乗のような、いつ計算しても値は同じだし、計算の状態の変化を引き起こさない場合(つまり値を返す以外の状態の変化である副作用(side effect)がない場合)、即ち函数定義としてプログラムを与えている場合には、再帰的プログラムを書く時に宣言的に考えることが可能です。またこのように考えた方がプログラミングを学びたての場合には理解しやすい人もいますし、すでに手続き的な考え方に慣れている人にとってはある意味新鮮な別の考え方であると思います。再帰呼び出しを行う函数を定義するときの考え方を以下に記述します。
- 最も基本的な引数の値の場合には、再帰呼び出しによって値を与えないようにする。
- 再帰呼び出しについては、呼び出された函数が正しい値を持つと仮定してよい。
- 再帰呼び出しの引数が、元の引数よりある意味簡単なものになっている必要がある。
- 再帰呼び出しのある函数は未定義の(手続き的に考えた場合には停止しない)場合がある。
1.はfib_rについてはfib_r(0),fib_r(1)の場合、fact_rについてはfact_r(0)の場合が該当します。2.はfib_r(x - 1)やfib_r(x - 2)、fact_r(x - 1)が正しい値を返すとしてプログラムを書いています。3.はこれらの場合、値が少ないフィボナッチ数や階乗の値を計算する方が、元のフィボナッチ数や階乗の値を計算するよりも簡単だと考えられます。4.について、2つの函数は負の数に対しては計算が止まりません。4があるため、正確には定義しているのは函数ではなく部分函数(partial function)であるということになります。
考え方の内3が一番曖昧で、どのような意味で簡単な引数で再帰呼び出しをするかは場合によって異なります。但し大抵の場合は直観的にわかる範囲の場合が殆どです。あらゆる場合に適用できるような、この部分の厳密な定式化はある意味不可能であることがわかっています。
但し以上の考え方は、あくまで副作用のない場合であり、次に出てくるタートルグラフィクスの再帰的な描画の手続きの場合、基本的にはやはり手続き的な考え方をすることになります。 手続き的に考える場合、仮引数などの局所変数は呼び出しごとに別物となります。
タートルグラフィクス¶
画面に図形を表示する演習を行うと興味を引かれる人が多いようであるという理由で、ここではタートルグラフィクスによる演習を行います。タートルグラフィクスとは、タートル(亀)の動きによりさまざまな図形を描くというグラフィクスの一方式です。いわゆるフラクタル図形等の描画を簡単に行うことができます。タートルグラフィクスは、それ自身を扱うのが容易で、しかもタートルグラフィクスの基本プログラムを記述するのも簡単なため、入門的なコースや説明でよく使われるものの一つです。
タートルグラフィクスにはJuliaのシステムに最初から用意されているLuxorに含まれているものを用いることにします。小さいプログラムを書けば簡単に使えます。 ただしWindows32bit版のJuliaなどでエラーが出る場合があり、 その場合には独自版のタートルグラフィクスプログラムを利用します。 後者はエラーが出ない場合にも利用できます。
タートルをJuliaのようなオブジェクト指向言語で実現する場合、タートルをオブジェクトとし、マルチタートルグラフィクスとするのが自然です。後で解説するライブラリではそのように記述しています。
# Pkg.add("ImageMagick") # 画像ファイルをinlineで表示するために必要。
Pkg.add("Images")
# Luxorを使う場合にはこのセルと次のセルを実行する。
# ただしWindowsの32bit版のJuliaだとエラーが出る場合があり、もしそうならLuxorは使用せず、
# 独自版の暫定Turtleグラフィクスプログラムを利用する(下記)。
# このセルはJuliaのインストールごとに一回実行する。
# Jupyterサーバの起動やnotebookの編集ごとに実行する必要はない。
# Luxor利用の場合、描画プログラムの初回実行でエラーが出、再実行すると描画される場合がある。
Pkg.add("Luxor")
# Luxorを使用するならこのセルも実行する。このセルはkernelの起動ごとに実行する。
using Luxor
clone(t) = Turtle(t.xpos, t.ypos, t.pendown, t.orientation, t.pencolor)
# Luxorを使わず、独自のタートルグラフィクスプログラムを使用するならこのセルを実行する。
# このプログラムとLuxorを切り替えるにはkernelをrestartする。
# これはLuxorが32bitのJulia処理系で(おそらく一時的に)うまく動かなかったから応急処置として作成した。
# Pkg.add("Images")
using Images
CanvasType = Array{ColorTypes.RGB{FixedPointNumbers.Normed{UInt8,8}},2}
function line(can::CanvasType,x1,y1,x2,y2,c)
x1,y1,x2,y2 = -y1,x1,-y2,x2
let (xs,ys) = size(can),
((xx1,xx2),(yy1,yy2)) = (0.5(xs + max(xs,ys)*[x1,x2]),0.5(ys + max(xs,ys)*[y1,y2]))
if xx1 < 1.0
if xx2 < 1.0 return
elseif xx2 > xs
yy2 -= (y1 - y2)/(x1 - x2)⋅(xx2 - xs)
xx2 = xs
end
yy1 += (y1 - y2)/(x1 - x2)⋅(1.0 - xx1)
xx1 = 1.0
elseif xx1 > xs
if xx2 > xs return
elseif xx2 < 1.0
yy2 += (y1 - y2)/(x1 - x2)⋅(1.0 - xx2)
xx2 = 1.0
end
yy1 -= (y1 - y2)/(x1 - x2)⋅(xx1 - xs)
xx1 = xs
elseif xx2 < 1.0
yy2 += (y1 - y2)/(x1 - x2)⋅(1.0 - xx2)
xx2 = 1.0
elseif xx2 > xs
yy2 -= (y1 - y2)/(x1 - x2)⋅(xx2 - xs)
xx2 = xs
end
if yy1 < 1.0
if yy2 < 1.0 return
elseif yy2 > ys
xx2 -= (x1 - x2)/(y1 - y2)⋅(yy2 - ys)
yy2 = ys
end
xx1 += (x1 - x2)/(y1 - y2)⋅(1.0 - yy1)
yy1 = 1.0
elseif yy1 > ys
if yy2 > ys return
elseif yy2 < 1.0
xx2 += (x1 - x2)/(y1 - y2)⋅(1.0 - yy2)
yy2 = 1.0
end
xx1 -= (x1 - x2)/(y1 - y2)⋅(yy1 - ys)
yy1 = ys
elseif yy2 < 1.0
xx2 += (x1 - x2)/(y1 - y2)⋅(1.0 - yy2)
yy2 = 1.0
elseif yy2 > ys
xx2 -= (x1 - x2)/(y1 - y2)⋅(yy2 - ys)
yy2 = ys
end
if abs(x1 - x2) >= abs(y1 - y2)
xx1,xx2 = round(Int32,xx1),round(Int32,xx2 - xx1)
if xx2 == 0
canvas[xx1,round(Int32,yy1)] = c
return
end
xx2 += xx1
s = sign(xx2 - xx1)
d = s⋅(y1 - y2)/(x1 - x2)
y = yy1
for x in xx1:s:xx2
if x < 1 || x > size(can)[1] || round(Int32,y) < 0 || round(Int32,y) > size(can)[2] @show y,yy1,yy2,d,x1,y1,x2,y2,x,xx1,xx2 end
can[x,round(Int32,y)] = c
y += d
end
else
yy1,yy2 = round(Int32,yy1),round(Int32,yy2 - yy1)
if yy2 == 0
canvas[round(Int32,xx1),yy1] = c
return
end
yy2 += yy1
s = sign(yy2 - yy1)
d = s⋅(x1 - x2)/(y1 - y2)
x = xx1
for y in yy1:s:yy2
if y < 1 || y > size(can)[2] || round(Int32,x) < 1 || round(Int32,x) > size(can)[1] @show y,yy1,yy2,d,x1,y1,x2,y2,x,xx1,xx2 end
can[round(Int32,x),y] = c
x += d
end
end
end
end
#
# Turtle Graphicsのプログラム
#
# Luxorのタートルグラフィクス部分に対し、資料の使い方でのおおよその互換性を目指している。
# ファイルを作らないし、全体での互換性は全くない。
#
function Drawing(xs,ys,_)
global canvas = convert(CanvasType,ones(ys,xs)*RGB(1,1,1))
end
background(_) = nothing
finish() = nothing
origin() = nothing
preview() = canvas
type Turtle
canvas::CanvasType
xpos::Float64
ypos::Float64
orientation::Float64
speed::Float64
pencolor::ColorTypes.RGB{FixedPointNumbers.Normed{UInt8,8}}
pendown::Bool
Turtle(x,y,pen,dir,rgb) =
new(canvas, x, y, dir, 2.0/maximum(size(canvas)), RGB(rgb[1]/255,rgb[2]/255,rgb[3]/255),pen)
end
function Forward(t::Turtle, d)
let rad = t.orientation/180.0⋅π
x, y = t.xpos+d⋅t.speed⋅cos(rad), t.ypos-d⋅t.speed⋅sin(rad)
if t.pendown line(t.canvas,t.xpos,t.ypos,x,y,t.pencolor) end
t.xpos,t.ypos = x,y
end
end
clone(t::Turtle) = let t1 = Turtle(t.xpos,t.ypos,t.pendown,t.orientation,(0,0,0))
t1.canvas,t1.speed, t1.pencolor = t.canvas,t.speed, t.pencolor
t1
end
Turn(t::Turtle, d) = (t.orientation += d)
Reposition(t::Turtle, x, y) =
let m = 0.5maximum(size(canvas)); t.xpos = x/m; t.ypos = -y/m; (x,y) end
Pencolor(t::Turtle, r, g, b) = (t.pencolor = RGB(r/255,g/255,b/255); t.pencolor)
turtlestack = []
Push(t::Turtle) = push!(turtlestack,clone(t))
Pop(t::Turtle) = let u = pop!(turtlestack); t.canvas = u.canvas; t.xpos = u.xpos; t.ypos = u.ypos;
t.orientation = u.orientation; t.speed = u.speed; t.pencolor = u.pencolor; t.pendown = u.pendown
end
Koch曲線、Hilbert曲線、Sierpinski曲線¶
タートルグラフィクスによっていわゆるフラクタル曲線を簡単に描くことが可能になります。なお、グラフィクスのプログラムは環境によって挙動が変化する場合があります。ここでは描画中の画像を見ることができず、結果をinlineで資料中にはめ込んだ形で見られる環境を想定しています。
なお以下のプログラムの実行時にLuxorが初回実行だと、precompileが行われ、エラーが出る場合があります。そのような場合に再実行すると、とりあえず以下のプログラムの表示が得られる場合があります。ただしLuxorの全機能を利用できる状態になっているかどうかはわかりません。
なおタートルグラフィクスの部分のプログラムは、描画ファイルをnotebookのファイルと同じ場所に書き込むようになっています。同名のファイルがあると上書きされます。場所やファイル名を変更したい場合にはDrawing(-,-,-)の3つ目の引数を変更してください。
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, l÷2, "jkoch.png") # キャンバスのファイル。÷は整数除算。0.5lとしても動作する。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
function koch(t, x) # returnがないのは函数ではなく手続きだから。つまり返り値がなく、副作用(この場合は描画)のみが結果となる。
if x <= 4.0
Forward(t, x) # タートルの向きにx進む。ペンが下りていれば描画される。
else
x /= 3
koch(t, x) # 再帰呼び出し
Turn(t, -60) # 左に90度向きを変える
koch(t, x)
Turn(t, 120) # 右に120度向きを変える
koch(t, x)
Turn(t, -60)
koch(t, x)
end
end
Pencolor(t, 0, 0, 0) # タートルの色をRGBで指定する。この場合は黒。
Reposition(t, -4l÷10, l÷10) # タートルの座標の設定。
koch(t, 8l÷10) # Koch曲線の描画。
finish() # 描画終了
preview() # 表示
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, l, "jhilbert.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
function hilbert(t,x,y,theta)
if x >= y
x /= 2
Turn(t,theta)
hilbert(t,x,y,-theta)
Forward(t,y)
Turn(t,-theta)
hilbert(t,x,y,theta)
Forward(t,y)
hilbert(t,x,y,theta)
Turn(t,-theta)
Forward(t,y)
hilbert(t,x,y,-theta)
Turn(t,theta)
end
end
Pencolor(t, 0, 0, 0) # タートルの色をRGBで指定する。この場合は黒。
Reposition(t, -4l÷10, 4l÷10) # タートルの座標の設定。
Turn(t,-90) # タートル上むきに。
hilbert(t, 384, 12, 90) # Hilbert曲線の描画。
finish() # 描画終了
preview() # 表示
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, l, "jsierpinski.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
function sierpinski(t,x,y,theta)
if x < y
Forward(t,x)
else
x /= 2
Turn(t,-theta)
sierpinski(t,x,y,-theta)
Turn(t,theta)
sierpinski(t,x,y,theta)
Turn(t,theta)
sierpinski(t,x,y,-theta)
Turn(t,-theta)
end
end
Pencolor(t, 0, 0, 0) # タートルの色をRGBで指定する。この場合は黒。
Reposition(t, -4l÷10, 4l÷10) # タートルの座標の設定。
sierpinski(t,768,6,60) # Sierpinski曲線の描画。
finish() # 描画終了
preview() # 表示
副作用と再帰呼び出し¶
この部分は少々普通ではない説明をしていますので最初は飛ばしてください。課題を解くのにも必要ないと考えられます。
上のプログラムでは再帰呼び出しを行なっていますが、函数には返り値がありません。即ち副作用のみのプログラムです。この資料ではこのような函数を手続き(procedure)と呼ぶことにします。この場合の副作用はウィンドウにタートルの跡を描きつつタートルの位置や向き、色を変更することです。このように副作用のみの場合には再帰呼び出しを行うプログラムの内容の理解やそれを書く場合にどのように考えればよいのでしょうか。これには2つの方法があります。
- プログラムの動作を手続き的に理解し、記述するという標準的な方法。
- プログラムの副作用をタートルへの操作の列であると考え、操作の列全体を結果とする宣言的なプログラムとして捉え直す。
ここでは2番目の理解の仕方を説明してみます。 手続き(函数)が呼び出され、ForwardやTurnなどの操作をタートルに行うのを、操作の列として求める函数だと捉えます。それらの操作は順序に意味がありますが、結合律を満たします。即ち$a_i$を個別の操作とすると、$(a_1,a_2),a_3$という操作と$a_1,(a_2,a_3)$という操作は操作として同じことです。また何もしない、という操作も考えられ、それがある種の単位元になっています。こうしてタートルへの操作の列を生成する宣言的なプログラムであると考えることができますが、これだけですと抽象的な説明であって具体性が不十分なので操作の列を生成するような宣言的なプログラムに書き換えてみます。但し$\lambda$式や後で説明するような概念のリストを先走って使っているので、この部分は飛ばしていただいても構いません。またこのような書き換えを行なうと実際に描画が行われる時刻が変わってくるので、その意味では元のプログラムと等価ではなくなります。
次のプログラムでは再帰的に定義されたsierpinskiという函数の代わりにsierpinski_mという副作用のない函数を定義しています。この函数はタートルへの操作の列(配列)を値として返します。但し後で実行できる形式とするために未説明の言語要素である$\lambda$式を使っています。変数への代入が行われていますが、これは一回だけの代入であり、mutableな変数として扱ってはいません。再帰呼び出しの際に同じ変数名の変数に何度も代入が行われますが、これもそれぞれが論理的に別の変数であり、宣言的なプログラムであることに変わりはありません。上のプログラムと見比べてみてください。
但しプログラムの最後のforの部分では、配列中の操作を全て行なって実際の描画を行なっています。この部分だけが手続き的なプログラムとなっています。
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, l, "jsierpinski.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス。
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成。ここまでは手続き的なプログラム。
function sierpinski_m(t,x,y,theta,a0)
if x < y
push!(copy(a0), (()->Forward(t,x))) # 実はcopyなしでpush!(a0,...)としても動作すると思われる。
else # しかし函数的であることをはっきりさせるためにcopyを入れた。以下同様。
x /= 2
a1 = push!(copy(a0),(()->Turn(t,-theta))) # push!(copy(x),a)は配列xの最後に要素aを置いた配列
a2 = sierpinski_m(t,x,y,-theta,a1)
a3 = push!(copy(a2),(()->Turn(t,theta)))
a4 = sierpinski_m(t,x,y,theta,a3)
a5 = push!(copy(a4),(()->Turn(t,theta)))
a6 = sierpinski_m(t,x,y,-theta,a5)
push!(copy(a6),(()->Turn(t,-theta)))
end
end
a1 = push!([],(()->Reposition(t, -4l÷10, 4l÷10)))
a2 = push!(copy(a1),(()->Pencolor(t,0,0,0)))
a3 = sierpinski_m(t,768,6,60,a2)
for i in a3 # 以下の部分は手続き的なプログラム。
i() # a3の各要素を描画操作として順に実行する。
end
finish() # 描画終了
preview() # 表示
オブジェクトとは¶
ここで改めてオブジェクト指向プログラミングについて説明しておきます。オブジェクトという概念はできるだけ何にでも当てはめられるようなものですので、必然的に抽象的な概念であり、説明も抽象的なものとなります。したがってこの節の内容を実感を伴って理解できない場合、ざっと読飛ばすだけで十分であり、あとでプログラムの具体例を理解してから再読されるとよいと思います。
また以下の説明は、単一ディスパッチのオブジェクト指向言語についてのものであり、Juliaにはそのまま当てはまりません。Juliaでは多重ディスパッチという方法で函数を定義し、オブジェクトが計算の主役からやや外れた形になります。しかしオブジェクト指向の歴史としては単一ディスパッチの方が先に現れましたので、基本として押さえておくのが望ましいです。
オブジェクトとは自分自身の局所的なデータを備え、計算を行うものです。また、他のオブジェクトとデータをやり取りします。やり取りするデータのことをメッセージと呼びます。
メッセージの解釈は各オブジェクトが自分自身で行います。各オブジェクトの局所的なデータは特に指定しない限り他のオブジェクトから見たり書き換えたりすることができません。局所的なデータを見たり書き換えたりできる場合があるといっても、それらもメッセージにより行います。基本的には見るためあるいは書き換えるためのメッセージへの反応の仕方を記述したプログラムは、メッセージを送る側ではなく、メッセージを受けるオブジェクト側が持っています。従って外側から見てあるオブジェクトの局所的なデータを操作しているように見えたとしても、外側からはそれらしく見えているだけであって実際にそうなのかどうかは当該オブジェクト自身にしかわかりません。
このように、データとそれへの操作方法をまとめて定義し、それらを外から直接見られなくすることをデータ隠蔽とかカプセル化と呼びます。このようにするとデータとそれへの操作のプログラムをまとめて取り替えることが可能になり、ソフトウェアの部品化が容易になるし、プログラマは部品の余計な内部構造まで考えなくてすみます。この概念はプログラミング言語の発展における重要な概念の一つです。
同種のオブジェクトをまとめたものをクラス(あるいは型(type))と呼ぶ場合があります。すなわち、クラスが同じオブジェクトは、保持している局所的データの種類と個数が同じで、メッセージへの反応の仕方を記述するプログラムも同じです。メッセージにはメソッドと呼ばれる処理プログラムを表す一種のタグ(荷札)がついており、メソッドごとに処理プログラムを記述します。クラス概念があるプログラミング言語では、局所変数やメッセージへの反応の仕方を記述するプログラムを与えてクラスを定義します。クラスを新たに定義する場合、既存クラスの記述を利用することが可能です。この機能をインヘリタンス(継承)と呼びます。
上記の説明ではオブジェクト達がメッセージをやりとりして計算を行うという見方を説明しました。しかしその場合、メソッドを函数名と捉え、メッセージを受け取るオブジェクトを各函数の最初の引数であると考えることも可能です。そのような考え方をした場合、最初の引数のオブジェクトのクラス(型)によって適用される函数(メソッド)の実体が変わってくる、ということになります。
Juliaの場合には、先述したように多重ディスパッチという概念に基づいています。これは上の段落の考え方をした場合に、最初の引数だけではく引数全体の型から適用される函数の実体が変わってくる、というように一般化したものになっています。そのような函数のことを総称函数(generic function)という場合があります。
Juliaの場合、データの型をtypeof(-)という函数で調べることができます。またmethods(-)により、函数のディスパッチについて調べることが可能です。
typeof(1),typeof(t),methods(!)
マルチタートルの例: 渦¶
使用しているタートルグラフィクスのライブラリではタートルを複数同時に使うことが可能です。タートルはそれぞれオブジェクトとして実現されています。以下の例では2つのタートルを使って色が異なる2つの図形を同時に描きます。タートルを2つ生成し、left、rightという変数に代入して操作を行います。例えばForward(left,i)とすればleftに入っているタートルにForwardの操作が行われます。
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, l÷2, "juzu.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
left = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
right = Turtle(0, 0, true, 0, (0, 0, 0))
Pencolor(left, 255, 0, 0) # タートルの色をRGBで指定する。この場合は赤。
Pencolor(right, 0, 0, 255) # 青。
Reposition(left, -l÷5, 0) # タートルの座標の設定。
Reposition(right, l÷5, 0)
for i in 0:400
Forward(left,i)
Turn(left,91)
Forward(right,i)
Turn(right,89)
end
finish() # 描画終了
preview() # 表示
木¶
以下は深さ優先で木を描くプログラムです。
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, 2l÷3, "jdtree.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
function dtree(t, depth, theta, length)
Push(t) # タートル位置と方向の保存
Forward(t, length) # 現在の方向に進める
if depth > 1 # 葉ではない場合
Turn(t, -theta) # 左に回転
dtree(t, depth - 1, theta, length/1.2) # 長さを一定の比率で縮める
Turn(t, 2*theta) # 右に回転
dtree(t, depth - 1, theta, length/1.2)
end
Pop(t) # タートル位置と方向を元に戻す
end
Pencolor(t, 0, 0, 0) # タートルの色をRGBで指定する。この場合は黒。
Reposition(t, 0, l÷3) # タートルの座標の設定。
Turn(t,-90) # 上向き。
dtree(t,8,15,120)
finish() # 描画終了
preview() # 表示
以下は木の分岐ごとにタートルをコピーして増やし、並列に木を描くプログラムです。但し描画の過程が見られないと差がわかりません。
# using Luxor # ライブラリLuxorを使用する。予め関連パッケージがインストールされていないといけない。
l = 1000 # キャンバスの大きさ
Drawing(l, 2l÷3, "jbrtree.png") # キャンバスのファイル。
origin() # キャンバス中央を原点(0,0)に
background("white") # 白色キャンバス
t = Turtle(0, 0, true, 0, (0, 0, 0)) # タートル生成
function brtree(ts, depth, theta, length)
ts2 = ts[:] # 現在のタートルのリストをコピー
for t1 in ts
Forward(t1, length) # 現在の方向に進める
if depth > 1 # 葉ではない場合
t2 = clone(t1)
Turn(t1, -theta) # 左に回転
Turn(t2, theta) # 右に回転
push!(ts2,t2)
end
end
if depth > 1
brtree(ts2, depth - 1, theta, length/1.2) # 長さを一定の比率で縮める
end
end
Pencolor(t, 0, 0, 0) # タートルの色をRGBで指定する。この場合は黒。
Reposition(t, 0, l÷3) # タートルの座標の設定。
Turn(t,-90) # 上向き。
brtree([t],8,15,120)
finish() # 描画終了
preview() # 表示
2つ目の課題¶
タートルグラフィクスのライブラリを冒頭でusingして図形を描くプログラムを作成し、メール本文にコピー&ペーストしてkadai08として提出せよ。図形は自分が選んだ、あるいは創作したものとしてよい。ただし描画のプログラムは自分で記述すること。また、kernel restart後に提出プログラム部分のみを実行し表示を確認すること。描画した画像ファイルを添付すること。ファイルそのものを探して添付してもよいし、Webページのinline画像として結果が表示されている場合、ブラウザの機能で画像をファイルとして保存できる。提出先やファイル内容等は前回と同じである。
これまでに学習したプログラミングの技法以外の技法も用いてもよい。Luxor、Julia言語のリンクを見たり、サーチエンジンでPython言語要素などを調べれば多数の解説サイトが見つかるので、それらを参照すればさまざまなプログラミングの技法やJulia言語の機能を知ることが可能である。
# kadai08 s1234 課題提出用IDを書き換え
#
using Luxor
# function 描画手続き
# 描画手続き呼び出し
finish() # 描画終了
preview() # 表示
配列¶
様々なプログラミング言語に出てくる基本的な概念の一つである配列について説明します。
配列とは、データが入る箱が並んだものです。並んだ箱の数を配列の大きさと言います。箱の位置を指定する数字のことを添字(index)と言います。箱の中に入る物は同じ種類のデータしか許していない言語もあります(静的型付けの言語)し、Juliaのように箱ごとに異なる種類のデータを入れられる(動的型付けの)言語もあります。例えば配列の中に配列を入れることも可能です。
a = [1,3,5,7,9] # 最初の要素が1、2番目の要素が3...という大きさ5の配列
length(a), typeof(a) # リストの大きさと型
[1,3,5,7,9]というのは最初の要素が1、2番目以下の要素が3,5...という大きさ5のリストで、上の文によりaという変数にリストが入ります。print(-)によりこのままの形で表示されます。
添字が1から始まるかそうでないかの違いを除き、他のプログラミング言語の場合とほぼ同様に以下のようになります。
a[1],a[4] # 添え字は1から始まる
a[1] = 10
print(a)
Juliaの配列はスタックやキューも兼ねている¶
a = [1, 2, 3, 4, 5]
print(a)
push!(a,6) # 配列の大きさを1増やし、最後にデータを入れる
print(a)
popfirst!(a) # 配列の最初のデータを取り除く。入れたデータを順に取り出す仕組みをキューと呼びます。ersion0.7より前ではshift!でした
print(a)
push!(-,-)、shift!(-)で配列をキューとして使えます。今の場合には、最初1,2,3,4,5というデータがこの順にキューに入っていたところ、最後に6というデータを追加し、その後キューから最初のデータである1を取り出しました。
pop!(a) # 配列の最後のデータを取り除く
print(a)
入れたデータを逆順に取り出す仕組みをスタックと呼びますpush!(-,-)とpop!(-)というメッセージで配列をスタックとして使えます。
配列のいろいろな操作¶
a = [1, 2, 3, 4]
b = [5, 6, 7, 8]
print(append!(a, b)) # 2つの配列をくっつける
indexin([6,2],a)
deleteat!(b,indexin([6],b)[1]) # 最初の要素6を配列bから取り除く
print(b)
Juliaでは配列を実引数として渡すといわゆる参照渡しとなるため、 それの要素を変更すると呼び出し側にも反映されます。
x = [1,2,3]
function test(y)
y[2] = 0 # 仮引数yは局所変数だが、配列xが参照渡しなのでxの中身を変更できる。
y = [] # ただしy自身を変更してもそれは大域変数xには影響しない。
end
test(x)
x
函数定義の中でglobal宣言しなければ、大域変数が更新されることは通常ありませんが、 それの中身の配列の要素等が変更されることはあり得ることに注意してください。
例題: エラトステネスの篩¶
ここでは配列を使った例題として、エラトステネスの篩(ふるい)と呼ばれる手法により、ある数までの素数をすべて求めてみます。以下がそのプログラムです。値0で数値を消したことを表しています。
n = 300 - 1
a = collect(1:n)
a[1] = 0 # 範囲をリストに変換して1に対応する最初の要素を0にする
for i in a
if i != 0 # 0以外の場合
for j in 2*i:i:n # i以外のiの倍数を消す:i:のiはjをiずつ増やすことを指定している
a[j] = 0
end
end
end
a = [ x for x in a if x != 0 ] # aの各要素に対し、それが0以外の時のみ結果のリストに入れる
for i in a # 内包表記はJuliaのversionが古いと使えない。
print(i,',')
end
このプログラムでは、最初に1つ0があり、その後2以上与えられた数までの数値を要素として持つ配列を2行目で作っています。この時点では、1は素数でなく、素数だとわかっているのは2だけで、3以降は素数である可能性がある数値が配列中に残っている状態です。ある添字の要素が0でなければその添字の値自身がその添字の要素として入っています。
4-10行目で、配列の各要素について、それが0でなければその数の2倍の添字位置からリストの最後までの、その数の倍数の添字位置の要素を0に置き換えるという操作を繰り返し行います。ここではループが2重になっていることに注意してください。
下から4行目は内包表記といわれるもので、合成数の位置に入っている0を配列から消しています。
3つ目の課題¶
3つ目のkadai09はオプションです。即ち、提出したい人だけが提出してください。
先の節である数nまでの素数をすべて求める方法を見てみました。今度はまず、ある数までの素数の表を求め、それを使って数mを素因数分解する函数factorを書いてください。mは、函数の引数として与えるようにしてください。また、出力の形式は以下のようなものとしてください。
[[素因数1, 個数1], [素因数2, 個数2], … ,[素因数k, 個数k]]素因数iの個数i乗をi=1,...,kについてすべて掛け合わせた結果がmとなります。また、個数iは1以上の自然数です。ただし、あらかじめ求めた素数の表が、mの分解に足りない場合には、その旨を出力するようにしてください。その場合、途中まで行える分解の結果も表示してください。
例えば[2,3,5,7]という素数の表を求めていた場合、53の素因数分解には7*7 < 53なので表が足りません。63の分解であれば3で2回割り切れて7となりますので分解できます。3339=3*3*7*53の分解は、3で2回割って7で割ると53となり、7*7<53なので表が足りませんが、[[3,2],[7,1],[53,1]]というところまでは分解できます。ただしこの場合には最後の53が素数かどうかはわからないということになります(今の場合にはたまたま素数です)。表が足りない場合には、素数かどうかわからない部分も指示するようにしてください。例えば「[[3,2],[7,1],[53,1]](ただし最後の因数は素数とは限りません)」などと出力すれば十分です。
これまでに学習したプログラミングの技法以外の技法を用いても構いません。
# e81234 kadai09
#
# function factor(m)