課題を提出する際には, 必ず動作確認を行ってください. またPandA記載の注意事項を守ってください. なお,*が付いた課題は,飛ばしてもその後の学習にあまり影響がありません. わからない時にはとりあえず飛ばして学習を進めて下さい.
S式
ここに至るまでにLISP(scheme)のプログラムをいくつか書いてみて, 括弧の非常に多いプログラムだと思われたことでしょう. それらのプログラムは,「S式(えすしき)」という表現方法で書かれています. LISPでは,プログラムもデータもテキストファイルではS式で表します.
LISPのインタプリタがS式で書かれたファイルの プログラムを実行したり,データを処理する場合には, まずS式で書かれたファイルを読み取ります. 読みとられたデータはLISPインタプリタの内部の表現方式で表されます. その表現方式は,文字列としてのS式ではなく,「2分木」です. インタプリタは2分木の各ノードを「セル」というデータで表します. 各セルには,他のセルあるいは次に説明するアトムを指すポインタが2つずつあります. また数値や関数名,変数名などは,読みとられると「アトム(atom)」というデータに なります.アトムは,木でいえば一番端の「葉」の部分に来ます.
S式は,インタプリタに読みとられると, セルが複雑に繋がり,一番端にそれぞれアトムが付いているような2分木になる わけです. この授業では,そのような構造のことを「セル構造」と呼びます. なお,セルは,2分木になっている構造ばかりではなく, 一部のセルが重複していたり(木でいうと葉以外の部分も重複している), ループになっているような構造も表すことができますが, 通常のS式を読みとった場合にはそういった構造ができることはありません. それに対し,プログラムが動作した場合にはループがあったり重複部分のある 構造ができる場合が多々あります. なお,S式を読みとった場合にも,葉の部分が重複するのは普通です.
LISPでプログラミングを行うには, インタプリタがセルとアトムをどのように繋いでS式を表現するかを 理解する必要があります. 言い替えると,S式を読みとった時にどのようなセル構造ができるのか 分かるようになるということです. また逆に,セル構造をインタプリタがどのように文字列として出力するかを 理解せねばなりません. この,S式とセル構造の関係を理解するところが,LISPの初心者にとっての第 一関門になります.
そういうわけで,今日の説明は授業の重要ポイントなのですが, 蹉きやすい箇所でもあります. 一度に完全に理解できなくてもプログラムをある程度書くことはできますし, 通常はそうやってプログラムを書いているうちにほぼ完全に理解できるようになります. したがってこの項目の内容があまり理解できないような場合には、 リスト処理のkadai09から先に提出することをお勧めします.
[kadai08](1) 次のセル構造のS式で, まったく省略されていないものとできるかぎり省略されたものを求めよ.
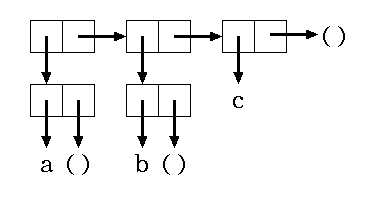
(2) 以下のS式をセルの構造に直せ.
(i) (p (q ( )) . r)
(ii) (define (plus x) (+ x 2))
(3) (2)のS式をまったく省略されていない形に直せ.
なお,セルを描くには罫線と矢印を使うとよい. 罫線は,次のコマンドでミニバッファに現れるメニューから選択できる. 「罫線」がメニューにない場合には,カーソルの上下を押せば,別の候補がメニューに現れる.
| M-x special-symbol-input |
矢印は,日本語入力モードで,以下のようにして書くことができる.
| ← | zh |
| ↑ | zk |
| → | zl |
| ↓ | zj |
次に罫線と矢印で描いたセルの例を示す. これをコピーして利用してもよい.
┌─┬─┐ │ │ │ └─┴─┘ ┌─┬─┐ │ │ ┼→ └─┴─┘ ┌─┬─┐ │ │ ┼→ └┼┴─┘ ↓
emacsを使用している場合にはpicture-modeを利用するとよい.
| M-x picture-mode |
picture-modeでは,文字を消去(C-d)しても,その後の部分が前にずれない. 逆に通常のモードのような動作をさせるには,C-c,C-dと入力する. またpicture-modeを抜けるには,C-c,C-cと入力する.
[参考] 矩形領域の内容を保存して利用する方法
- 矩形を指定する.
矩形の左上角と右下角によりリージョン (C-@によりカーソル位置にマークを付け、その後カーソルを移動する。 マークとカーソルの間の領域をリージョンと呼ぶ)を設定する. - 矩形の内容をレジスタに保存する.
C-x r r
のあと,レジスタ名(1文字)を適宜入力する.
(類似したコマンドにC-x xがある.これは(矩形でなく)通常のリージョンの内容をレジスタに保存する) - レジスタの内容を取り出す.
適当な場所で,
C-x g
リスト処理
[kadai09]
1-3についてはすべてに答えよ.加えて,4,5のいずれかについて答えよ. ヒントを参照すると,基本的な関数の説明がある.
- リストxのn番目の要素を返す2引数関数(nthcar n x)を定義せよ.
ただし第1引数で0以下が指定された場合には,1を指定した場合と同じ結果を返すものとする.
またxの最後の要素よりも後が指定された場合は,『( )』を返すものとする.
lengthを使用しないこと.
;; 動作例 ==> (nthcar 1 '(a b c (d e))) a ==> (nthcar 3 '(a b c (d e))) c ==> (nthcar 4 '(a b c (d e))) (d e) ==> (nthcar 0 '(a b c (d e))) a ==> (nthcar 6 '(a b c (d e))) () ==> (nthcar 2 '()) () ==> (nthcar 0 '()) () - リストの長さを返す1引数関数(listlen x)を定義せよ.
ただし,lengthを用いないこと.
;; 動作例 ==> (listlen '(a b c)) 3 ==> (listlen '(a b (c d e))) 3 ==> (listlen '()) 0 - 与えられたリストが0個以上の数値要素だけからなるリストであれば真(#t),
そうでなければ偽(#f)を返す1引数関数(number-list? x)を定義せよ.
;; 動作例 ==> (number-list? '(1 -2.3 4/5 6+7.8i)) #t ==> (number-list? '(5 4 (3 2 1))) #f ==> (number-list? '()) #tデータが数値かどうかを判定するには,次の関数を用いればよい.number?
- 自然数のリストが与えられたとき,リストの最大の要素を返す1引数関数(maximum x)を定義せよ.
なお,空リストの場合は,0を返すものとする.
また,組み込み関数maxを使用しないものとする.
;; 動作例 ==> (maximum '(1 4 3 2 5 0)) 5 ==> (maximum '(1)) 1 ==> (maximum '()) 0 - 真偽値のリストが与えられたとき,リストに#tが一つでもあれば#tを返し,
それ以外の時には#fを返す1引数関数(or-list x)と,
すべてが#tの時のみ#tを返し,他の時には#fを返す1引数関数
(and-list x)を定義せよ.
なお,空リストの場合は,それぞれ#fと#tを返すものとする.
;; 動作例 ==> (or-list '(#f #f #f #t #f)) #t ==> (or-list '(#f #f)) #f ==> (or-list '()) #f ==> (and-list '(#f #f #f #t #f)) #f ==> (and-list '(#t #t)) #t ==> (and-list '()) #t
[kadai10]
(1,2),(3,4),(5,6)についてはそれぞれいずれかについて答えよ. 7以降についてはすべてについて答えよ.
- 数値リストの各要素を2乗したリストを返す
1引数関数square-listを定義せよ.
;; 動作例 ==> (square-list '(1 2 3)) (1 4 9) ==> (square-list '()) () - 真偽値のリストの各要素を反転したリストを返す
1引数関数not-listを定義せよ.
;; 動作例 ==> (not-list '(#t #f #t)) (#f #t #f) ==> (not-list '()) () - 数値リストの各要素とその次の要素との差分のリストを返す1引数関数
fdiffを定義せよ.ただし,リストの最後の要素については,差分は
とらないものとする.したがって,差分のリストは与えられたリストに較べ
て要素が一つ少なくなる.なお空リストに対しては,空リストを返すものとする.
;; 動作例 ==> (fdiff '(1 2 3 2 1)) (1 1 -1 -1) ==> (fdiff (fdiff '(1 2 3 2 1))) (0 -2 0) ==> (fdiff '(1)) () ==> (fdiff '()) () - 真偽値のリストの各要素とその次の要素との排他的論理和のリストを返す
1引数関数bdiffを定義せよ.ただし,リストの最後の要素については,
排他的論理和を取らないものとする.したがって,結果のリストは与えられた
リストに較べて要素が一つ少なくなる.なお空リストに対しては,空リストを
返すものとする.
;; 動作例 ==> (bdiff '(#t #t #f #t #f)) (#f #t #t #t) ==> (bdiff (bdiff '(#t #t #f #t #f))) (#t #f #f) ==> (bdiff '(#t)) () ==> (bdiff '()) () - 与えられたリストから数値要素だけを取り出したリストを返す
1引数関数number-elementsを定義せよ.
;; 動作例 ==> (number-elements '(1 a 2 b c 3)) (1 2 3) ==> (number-elements '(5 4 (3 2 1))) (5 4) ==> (number-elements '(here there and everywhere)) () ==> (number-elements '()) () - 与えられたリストから真偽値の要素だけを取り出したリストを返す
1引数関数b-elementsを定義せよ.
;; 動作例 ==> (b-elements '(#t a #f 2 c )) (#t #f) ==> (b-elements '(#t #f (#t #f #t))) (#t #f) ==> (b-elements '(here there and everywhere)) () ==> (b '()) () - 二つのリストをつなぎ合わせる2引数関数(join x y)を定義せよ.
ただしappendは用いないこと.
;; 動作例 ==> (join '(this is) '(a book)) (this is a book) ==> (join '(linux freebsd solaris irix) '()) (linux freebsd solaris irix) ==> (join '() '(ferrari williams mclaren)) (ferrari williams mclaren) - 与えられたリストの要素を逆順にする1引数関数reverse-listを定義
せよ.必要であれば,上で定義したjoin,およびlistを用
いてもよい(これらを用いないで定義することもできる).
なお,reverseは用いないこと.
;; 動作例 ==> (reverse-list '(1 a 2 b c 3)) (3 c b 2 a 1) ==> (reverse-list '(5 4 (3 2 1))) ((3 2 1) 4 5) ==> (reverse-list '()) ()
[kadai11opt]
硬貨(1円,5円,10円,50円,100円,500円)を用いて,n円を両替する方法が何 通りあるかを求める1引数関数changesを定義せよ.なお両替に利用する 硬貨の枚数は1枚以上とする.すなわち,(可能であれば)n円を1枚の硬貨で 「両替する」場合も含める.たとえば,10円の場合は,次の4通りとなる.
1円10枚 1円5枚と5円1枚 5円2枚 10円1枚
;; 動作例
==> (changes 10)
4
==> (changes 50)
37
==> (changes 100)
159
==> (changes 500)
19162
==> (changes 1000)
248908